2 Dimensional Geometry

The word “geometry” calls to mind two- and three-dimensional shapes and the discovery of their properties.  These properties already exist in the world.  It is the mathematician’s job to uncover them, much like a great explorer.  In order to be a great explorer, we need to have an open mind, ask questions and solve problems.

Before solving geometric problems, we must be familiar with the language of geometry. Our students have created slide presentations to familiarize you with terms specific to our unit on geometry.  See student work here, here and here.

We study four aspects of two-dimensional geometry in 7th grade.

Angle Relationships

Angles are all around us.  The relationships between angles help create designs and are used in a plethora of careers.  In this unit we concentrate on the following angle relationships:  complementary angles (angles that add up to 90 degrees), supplementary angles (angles that add up to 180 degrees) and vertical angles (angles that are opposite and equal to each other).

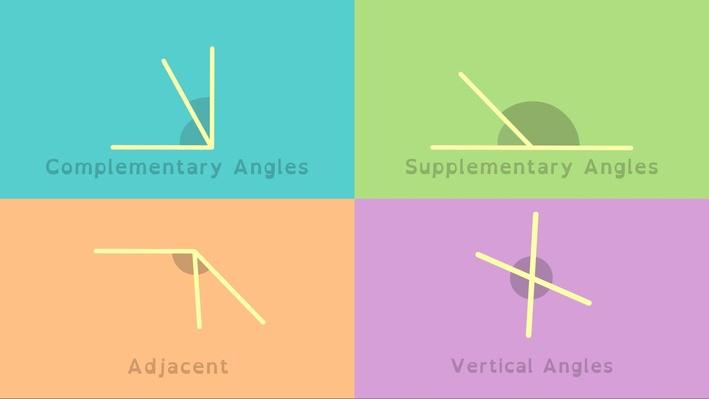
Click here to practice identifying these angles.

Using these relationships, students are able to build equations to find missing angle measures.

Here is a video for more on these angle relationships.  Click here to practice solving for missing angles.

Triangle Measurements

Students have been using triangles since preschool.  They are familiar with the fact that a triangle is a closed shape which is formed by 3 sides. In this unit these sides are further defined  as line segments.  The points of intersections of the sides of the triangle are called the vertices of the triangle. The corners formed at the vertices are called the angles of the triangle.

So, in a triangle, there are 3 sides, 3 vertices and 3 angles.  

Here, ΔABC has Sides : AB, BC, CA Vertices:  A, B, C Angles: ∠BAC, ∠ABC , ∠BCA.

Students tested the triangle inequality theorem, which states the sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Click here for a video tutorial on this theorem.

With protractors, students discovered that the sum of all the angles in a triangle is 180 degrees.  This is known as the triangle angle sum theorem.  Using this knowledge students were able to create equations and solve for missing angle measurements.

Click here to watch an example of how this theorem works.  Ready for some practice?  Click here to practice finding missing angles.

Area and Circumference of Circles

Working with circles is different than working with polygons.  For one thing, students become reacquainted with that unique ratio that exists in relation to all circles :

Pi is the ratio of the circumference to the diameter of any circle.  We use this ratio in the formulas to find both area (number of square units within a circle) and circumference (distance around a circle).

Click here to solve some practice problems involving finding the area and circumference of a circle.

Area of Composite Figures

Ever notice that some figures are comprised of a combination of shapes? These types of figures are called composite figures.

Take a look at this video showing composite figures all around us.  In this unit students learn to separate these composite figures into familiar shapes, and to use the area formulas they already know to find the area of these complex shapes.  

Here’s a video explaining how to separate these figures.  Try some on your own… click here.

Please feel free to comment on this blog.  Good luck!